DNAの二重らせんは 黄金比の１．６１８０３３９に近い

黄金比とは「人間が最も美しいと感じる」といわれている比率です。

 

黄金比は、特にヨーロッパでは古くから最も美しい比率として親しまれており、美術品に活用されてきました。

 

例えば、著名な彫刻、ミロのビーナスや、歴史的建造物といわれるパリの凱旋門、ギリシア遺跡 パルテノン神殿などにも、黄金比の比率が使われています。

 

 

黄金比は、特にヨーロッパでは古くから最も美しい比率として親しまれ美術品に活用されてきました。

 

例えば、古代ギリシアで制作された女性像「ミロのヴィーナス」

 

イタリアの有名な画家であるレオナルド・ダ・ヴィンチ「モナリザ」の顔の横と縦の比が黄金比になっており

 

「最後の晩餐」の構図にもいくつかの黄金比が使用されているようです。

 

其の他、パリの凱旋門、ギリシア遺跡 パルテノン神殿などにも、黄金比の比率が使われています。

 

一般的な「名刺」のサイズは55×91mmで、「1:1.65」ほどになるといわれ、まさに黄金比であり、

 

クレジットカードなどのカード類も「53.98×85.60mm」なので黄金比に近い

 

「1:1.58」であるといわれています。

 

また、世界的大企業、Apple社とGoogle社のロゴも、黄金比であることは有名な話ですね。

 

 

「黄金長方形」は縦と横の比率が「1：1.618」の黄金比となっている長方形のことをいいます。

 

 

著名な美術品からAppleやGoogleのロゴまで、さまざまなものに利用されている黄金比。

 

この黄金比は、デザインする際などに、図形が使われることが多くあります。図で表すと次のようになります。

 

 

 

 

 

 

 

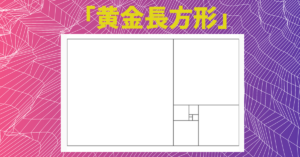
この黄金長方形を作るには、まず一つの黄金長方形を作った後、

 

その短辺と等しい長さの辺を持つ正方形を作り、その新しく生まれた黄金長方形について、

 

同じように短辺と等しい長さの辺を持つ正方形を作って、それを何度も繰り返していくと、

 

最終的に図のような長方形になるのです。

 

 

 

 

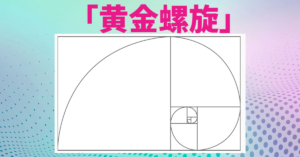
そして、この黄金長方形の黄金長方形の内部にあるすべての正方形の角の点をなめらかにつないでいくと

 

図のような黄金螺旋を作り出すことができます。

 

 

 

 

 

 

 

 

イタリアの数学者フィボナッチ(1170~1259年頃)が紹介した数列を「フィボナッチ数列」と言います。

 

１、１、２、３、５、８、１３、２１、３４、５５、８９、１４４、２３３、３７７…

 

「どの数字も前２つの数字を足した数字」という規則の数列です。

 

この数字は、実は自然界に多く潜んでいます。

 

 

１＋１＝２

１＋２＝３

２＋３＝５

３＋５＝８

５＋８＝１３

８＋１３＝２１…

 

 

 

自然界の数を拾い出していくと、

 

5、8、13、21、34の数列が導き出される。

 

 

この黄金らせんは、オウム貝の貝殻、バラの花びらが複数重なっている状態描く曲線など

 

 

 

 

 

 

いずれも黄金螺旋に近しいといわれているのです。

 

黄金比は「１：(1+√5)÷2」=1.618…です。

 

これはフィボナッチ数列の隣り合う数字の比と一致します。

 

例えば、植物には数や形の法則が隠されています。

 

 

ひまわり：ひまわりのタネの部分にも螺旋があり、右回りに21列、左周りに34列

 

ひまわり花：時計回りと反時計回りに配列された黄金螺旋で構成されています。

 

 

松ぼっくりの鱗模様は螺旋を描きながら回転しています。

 

 

サボテンの棘も螺旋を描いています。

 

右回りに13列

左周りに21列

 

 

これら「螺旋(らせん)」は「生命の曲線」といわれ、自然界であらゆるところで観察されます。

 

 

 

人のDNAの2重螺旋構造もこれが関係あるようです。

 

 

 

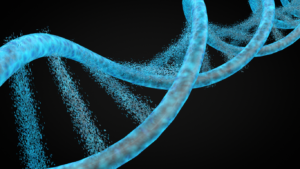
DNA の二重らせんは、お互いにらせん状にからみついた 2 本のポリヌクレオチド鎖をもちます。

 

デオキシリボース と リン酸基 が交互に並んでいる。

隣接する塩基の間隔は 34オングストローム。

1オングストロームは0，1ナノメートル。

幅21オングストローム

 

 

この比率は、１．６１９０４７６＝黄金比の１．６１８０３３９に近い。

 

 

このように、生命には法則があり、それは数字や幾何学で表すことができるといわれているのです。